Recursividad

Algoritmos 7: Recursividad

Recursividad (algoritmos recursivos), algo que se da cuando una función se invoca a sí misma. Se suele usar en problemas de naturaleza recursiva, para reemplazar las estructuras repetitivas, creando algoritmos cortos y elegantes.

Introducción a la Recursividad

La recursividad es una técnica compleja, no es fácil de dominar, pero es útil en más de una ocasión.

Viene de la mano del tema funciones, así que recordemos un poco este tema.

Funciones

Una función es una herramienta que nos permite aislar un bloque de código,  escribirlo una sola vez, usarlo en donde queremos las veces que necesitemos, simplemente invocando a la función.

Definición

Una función tiene la forma:

tipo_dato_retorno nombre_funcion (tipo_dato1 param1, tipo_Dato2 param2….)

Una función puede invocar, otra función por ejemplo: tenemos una función que busca el mayor en un ARREGLO de enteros.

Otra que busca al menor:

Estos ejemplos los explico en detalle en el artículo de arrays.

Tenemos la función buscar, que mediante el criterio recibido, invoca a la función que retorna el mayor o a la que retorna el menor.

Dentro de la función buscar invocamos a otras funciones, algo que se hace normalmente.

Para más detalles, este es el artículo sobre funciones.

Invocándose a sí misma

Una función puede invocar otras funciones… entonces… ¿se puede invocar misma?? la respuesta es SÍ!!!.  Es lo que se conoce como recursividad.

La funcionA tiene una variable resultado, la variable de retorno, y dentro del cuerpo de la función se invoca a ella misma, asignando el valor de retorno a la variable resultado.

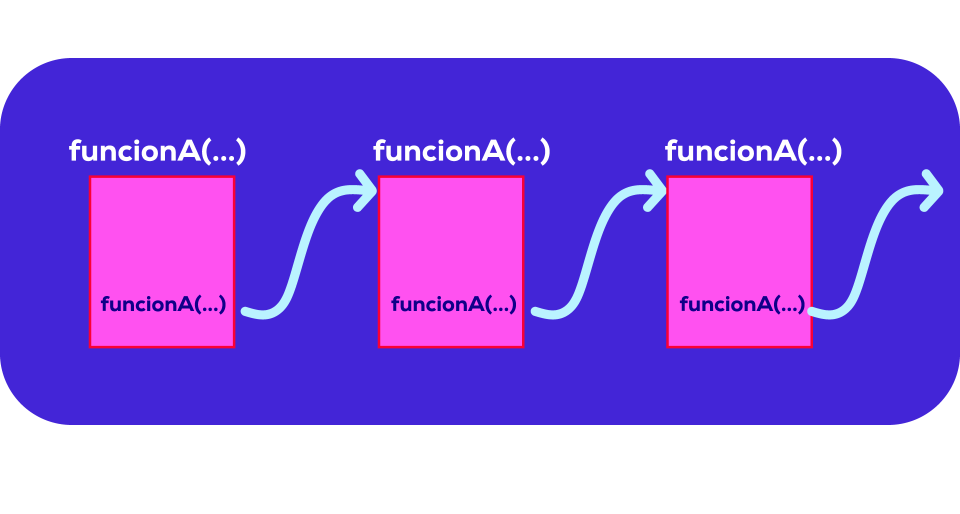
Paso a paso

• Se ejecuta la funcionA.
• Se llega a la línea en la que se invoca a la funcionA, se ejecuta una nueva instancia de la funcionA
• Dentro de esta nueva instancia de la funcionA, se llega a la línea en la que se invoca a la funcionA, se ejecuta una nueva instancia de la funcionA.
• Sigue el mismo comportamiento se vuelve a invocar a la funcionA, y así por los siglos de los siglos.

Lo que notamos es que necesitamos poner una condición de corte, para que se deje de ejecutar esta invocación recursiva, y evitar que nuestro programa quede ejecutando eternamente

Alternativa a ciclos

La recursividad es una alternativa a las estructuras repetitivas o bucles, pero se usa principalmente en problemas de naturaleza recursiva.

En matemática por ejemplo, se puede aplicar a la función factorial, a la serie Fibonacci (esta serie es muy conocida en el ambiente de la programación).

Pero también tiene aplicaciones fuera del ámbito de la matemática, por ejemplo, imaginemos un menú de opciones,  como cuando llamamos por teléfono a un servicio, a un Banco… donde estamos horas navegando en el menú, nos piden que presionemos dígitos, vamos navegando entre menús, avanzando, volviendo atrás. Este es un caso de naturaleza recursiva, un menú con submenús adentro,  permitiendo que se vayan agregando más de acuerdo a la necesidad.

Ejercicio

Armar un algoritmo para calcular el factorial de un número, sabiendo que la función Factorial se define como:

Primero debemos entender algo…¿Dónde entra la recursividad acá?

Vamos a un caso puntual, calculemos el factorial de 5 (se escribe 5!):  

• 5! equivale a 5.4.3.2.1, es lo mismo que 5 x 4! …
• 4! es igual a 4 * 3! ….. 
• 3! es 3 * 2! ….
• 2! = 2 x 1! …
• 1! = 1 * 0! ….

Entendiendo esto, podemos generalizar, el factorial de un número es: n * (n-1)!

Así que en términos generales podemos ver que la formula es n! es:

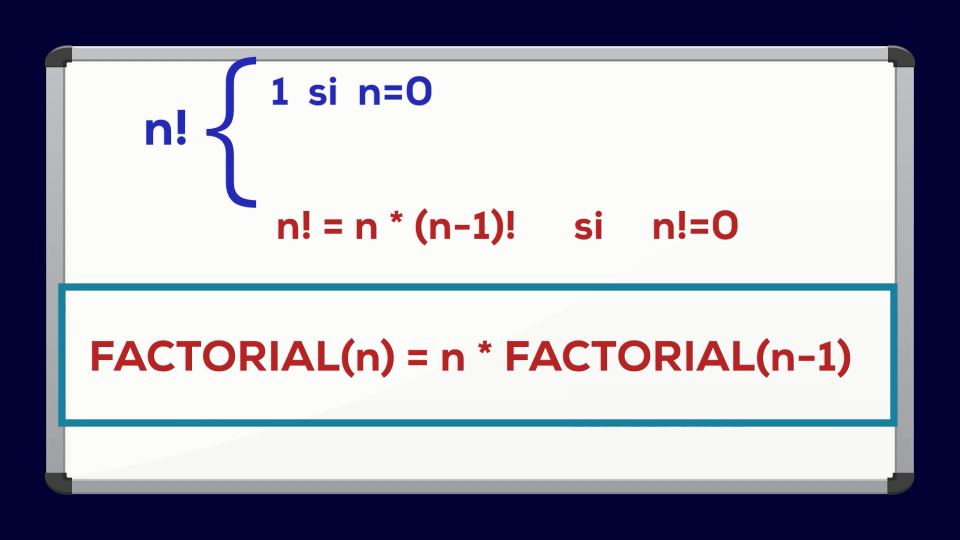
• 1, si n es 0
• n*(n-1)!, si n es dinstinto de 0

Si la expresamos en términos recursivos sería:

FACTORIAL (N) es N * FACTORIAL(N – 1)

Si la escribimos en pseudocódigo la función quedaría:

La función factorial recibe por parámetro un entero y retorna un entero. Tenemos que evaluar dos casos: por definición, si n es cero la función retorna 1, sino retorna n por el factorial de n-1, acá esta la invocación recursiva.

Pero… ¿cuál es la condición de corte acá? El n=0, cuando haga el factorial de 0 se llega al final de las invocaciones.

Proceso gráfico

Vamos a ver el proceso gráfico en detalle para el Factorial de n igual a 3

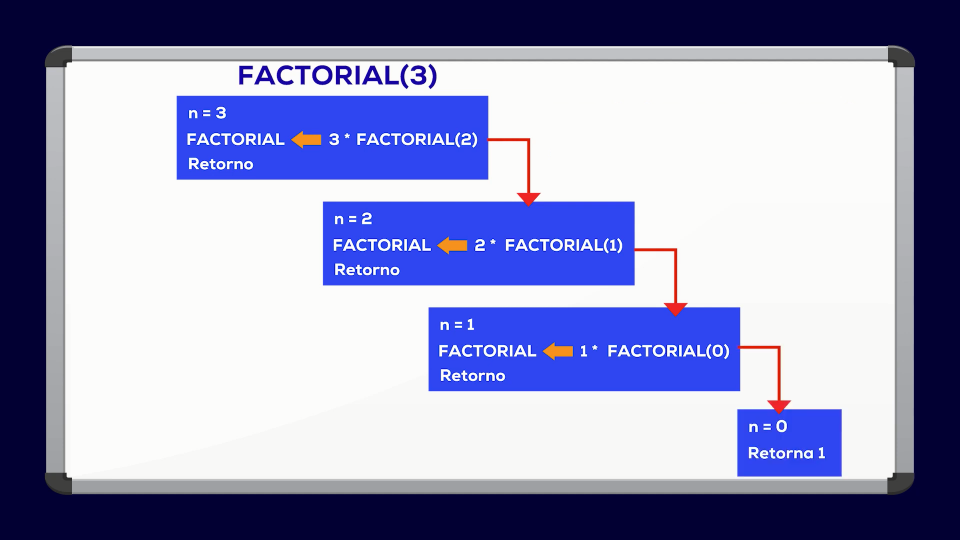
• Se ingresa a la función factorial, n vale 3, distinto de cero, así que va a la linea que invoca a factorial de n-1, factorial(2).
• Cuando vuelva de la invocación va a retornar 3 * el valor que reciba de la invocación a factorial (2).
• Ingresa a factorial(2), n es 2, disntinto de cero, por lo que invoca a factorial(1).
• Ingresa a factorial(1) y ejecuta la linea de 1 * factorial (0). Invoca a factorial(0).
• Ingresa a factorial(0), con n igual 0. En esta caso se cumple que n es cero,  así que retorna 1, saliendo de la función.
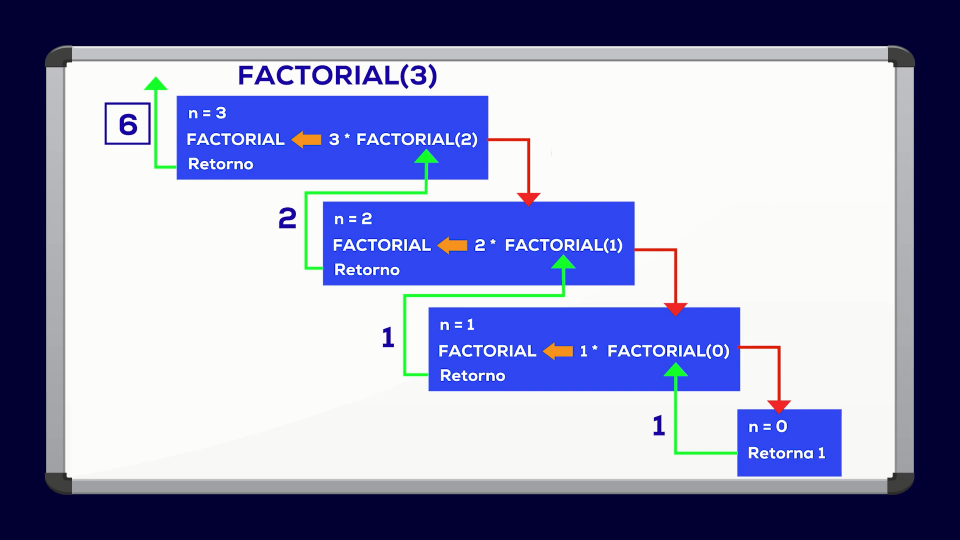
• Vuelve a la invocación anterior, ejecuta 1 * el resultado de la función factorial(0), que vale 1, por lo que ejecuta 1 * 1 = 1,  y retorna ese resultado.
• Vuelve a la invocación anterior, retornando 1. el caso de n igual 2 ejecuta 2 * 1=2 y lo retorna.
• Vuelve a la invocación anterior de n igual 3, hace 3 * 2 = 6 y lo retorna, terminando el ciclo de ejecución, siendo 3! = 6.

Ejercicio

Vamos a hacer otro ejercicio, el de la serie Fibonacci, es una serie de números de la siguiente forma 1, 1, 2, 3, 5, 8, 13, 21, 34…

La función matemática que expresa la serie de Fibonacci (fib) es:

fib(1) = 1

fib(2) = 1

fib(n) = fib(n – 2) + fib(n – 1) para n > 2

¿Cómo podemos escribir esta función en pseudocodigo? que por naturaleza es recursiva:

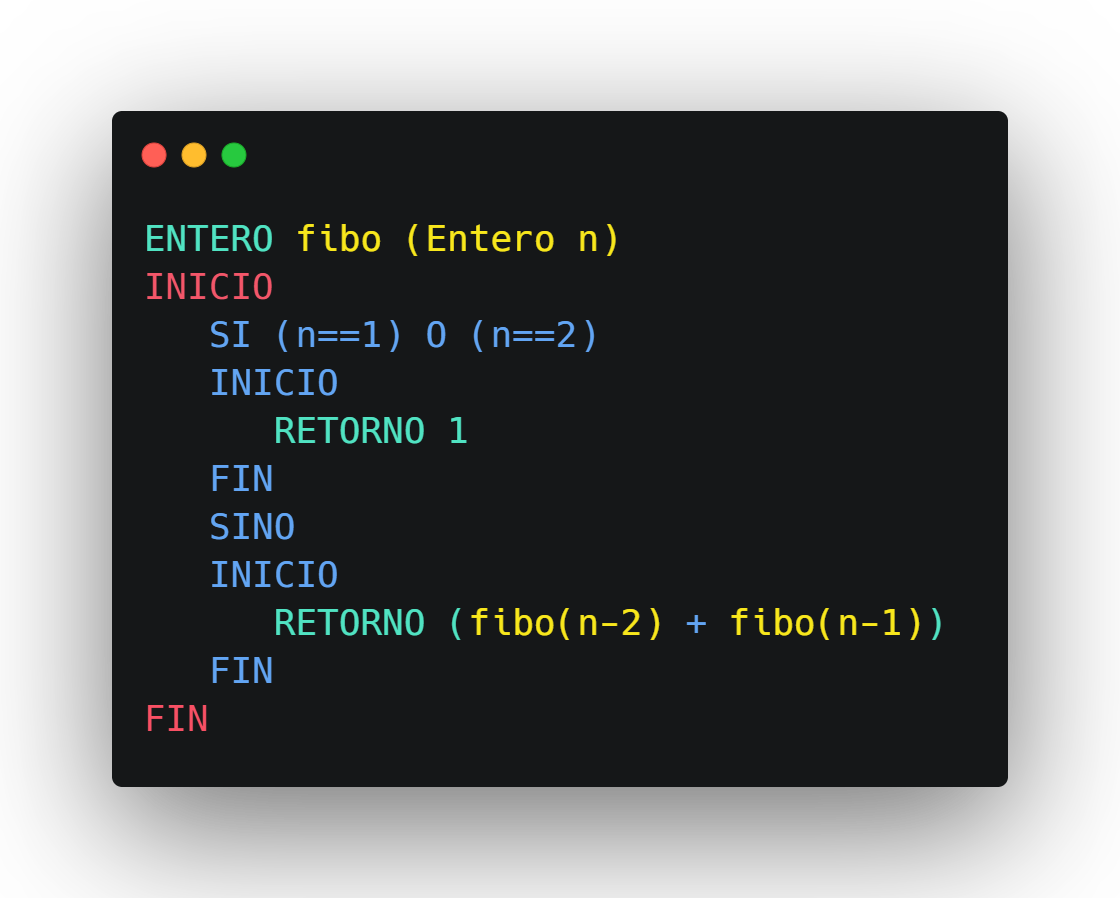
Creamos la función fibo que recibe un entero y retorna un entero.

Tenemos que considerar los casos n=1 y n=2

• si n es 1 retorna 1
• si n es 2 retorna 1

Lo podemos escribir directamente, si n es 1 o n es 2  retorna 1, sino retorna fibo de (n-1) + fibo de (n-2).

En Resumen

En este artículos vimos recursividad, una alternativa a las estructuras repetitivas o bucles. Las funciones factorial y fibonacci también se podían haber implementando con bucles.

Hay que tener en cuenta que la recursividad tampoco es lo más performante, porque en cada invocación tiene que cargar la función completa en memoria,  pero la principal ventaja es que nos lleva a algoritmos cortos y elegantes, con menos lineas de código.

También se usa mucho para recorrer estructuras de arboles, un tema importante que más adelante vamos a ver.

En el próximo artículo veremos diagramas de flujo, una herramienta para visualizar los algoritmos.